这……好吧。 只要用数学推导就可以出来，但是大家都很懒。 我们先拍张照片方便讨论。 （顺便说一句，这是一个面试问题，对吧？）

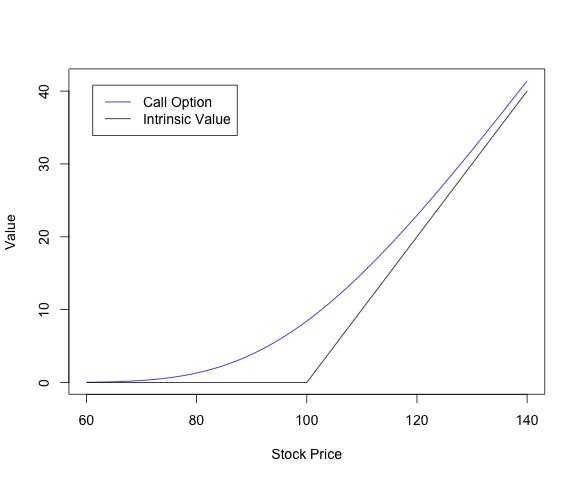
所谓时间价值（Time Value）就是期权价格与期权内在价值（Intrinsic Value）之间的差额。

TV = C(S_t) - IV(S_t)

为了方便讨论，我以看涨期权为例。 了解后，Put也是一样。 这里假设您的期权的收益函数是关于股票价格的连续函数。 原因在答案最后有解释。 正如你从我的公式中看到的，我假设利率、波动性、到期时间和行权价格是常数。 不过，我下面说的并不需要这个假设，只是为了讨论方便而已。

好吧，让我重写一下上面的公式

TV = C(S_t) - \text{max}\{S_t - K, 0\}

当S_t \le K时，内生值为零。 此时我对方程左右两边的S_t求导，得到

\frac{d TV}{d S_t} = \frac{d C(S_t)}{d S_t} = \Delta(S_t) \in [0,1)

这时候，等式右边不就是期权的Delta吗？ 由于这是一个看涨期权，所以它的delta是非负的，并且delta必须小于1。（我在答案的最后有解释）

现在我们考虑一下当K">S_t > K时，这时候期权的内生价格就变成了S_t - K，对吗？将方程两边求导，得到：

\frac{d TV}{dS_t} = \Delta(S_t) - 1 \in [-1,0)

让我总结一下

\开始{案例}

\ge 0 & S_t \le K \\

\end{cases}">\frac{dTV}{dS_t}

\开始{案例}

\ge 0 & S_t \le K \\

\结束{案例}

换句话说，当期权处于价外（Out of Money）状态时，期权的时间价值随着股票价格的增加而增加，而当期权处于价内（in the Money）时，期权的时间价值随着股票价格的增加而增加。股票价格。 并减少。 所以……当期权处于平价状态（At the Money）时，时间价值达到顶峰。

就是这样，我本来可以更严谨一些，但是我太懒了……如果看跌期权（Put）的情况反过来就更好了。

为什么Delta的绝对值不能超过1？

你可以使用期权定价公式看到Delta小于1，但我们也可以直观地理解为什么一定是这样。 因为期权含有杠杆，这是因为回报曲线是非线性的。 那么，更简单的说，你看上图期权的收益函数，也就是内生价值曲线，它的最低值为0。也就是说，相对于股票，你的最大损失是一定的。 Delta代表期权价格相对于股票价格的变化率。 由于期权内生价值的非线性，当股票价格发生变化时，期权价格的变化小于股票价格的变化。

为什么我们需要假设期权的收益函数是股票价格的连续函数？

当该函数不连续时，例如数字期权，导数不存在并且是无限的。 此时Delta的绝对值不再小于1，因为此时Delta还没有定义。

更多资讯请访问我的专栏-梗犬财经