[摘要] 霍华德·马克斯观察到的“周期”波动曲线是客观存在的，投资者的投资收益完全取决于买入点和卖出点在周期波动曲线上的相对位置。 因此，想要投资成功，首先要解决两个关键问题。 一是获得与股价同步的周期性波动曲线，二是准确确定当前在周期性波动曲线上的具体位置。 本文从数学上证明了马克思所描述的“周期”波动隐藏在股价曲线中，并提供了“周期”波动的范围、获取方法和仓位判断方法，可以为投资者提供准确的买卖机会和认识到最好的投资目标是在熊市底部买入，在牛市顶部卖出。

这篇文章补充了马克思的《循环》。 本文将“循环”从感性认识提高到理性认识，从定性分析提高到定量分析，从经验总结提高到科学理论。 本文是马克斯50多年投资实践经验科学抽象而形成的理论。 麦克斯50多年的投资实践成果是对本文科学理论的充分实验验证。

参见：Max的新书《把握市场周期》

早在100多年前，发明道琼斯指数、创办《华尔街日报》的查尔斯·道就发现股票价格的波动由基本波动、次级波动和每日波动三种波动组成。 1902年查尔斯·道去世后，汉密尔顿和雷亚将道在《华尔街日报》上发表的一系列文章概括为“道氏理论”。 由于查尔斯·道生前只观察了5年的股市数据，他并没有发现股价波动的长期线性趋势。

第一位获得诺贝尔经济学奖的美国经济学家萨缪尔森对美国过去半个世纪的股指回报率进行了实证研究，发现股指回报率每年平均线性增长率为8%。 ，并于1965年建立了带有漂移的股票价格的几何布朗运动模型。因此，实际股票价格是由四个不同时期的波动叠加而成的：如图所示的线性趋势（零频波动）、基本波动、次级波动和日波动如图1所示。股票价格可以用以下公式表示：

股价=线性趋势+基本波动+次级波动+每日波动

马克思《周期》中提到的周期性波动，本质上是指《道氏理论》中的基本波动。

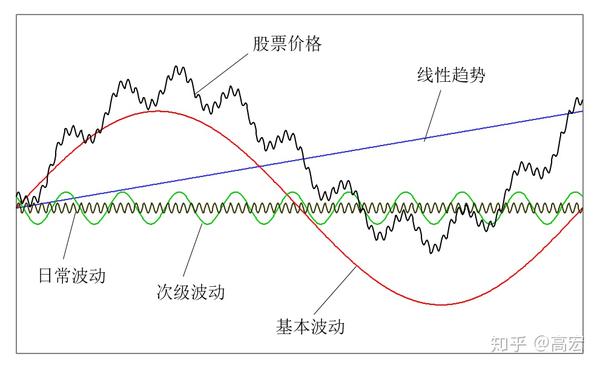
图1 股价波动的四种类型

1. 道氏理论简介

查尔斯·道通过对股票市场的观察发现，股票价格的波动是由以下三种不同程度的波动组成的：

基本波动：周期为1年以上的波动，看起来像海上的潮汐现象，波动幅度最大。 当基本面波动上升时，就形成股市牛市，当基本面波动下跌时，就形成股市熊市。 例如，2005年至2007年的牛市期间，上证指数从2005年6月6日的998.23点上涨到2007年10月16日的6124.04点，涨幅达613.48%。 马斯克所说的“周期”中的市场波动指的是基本波动。 基本面波动具有很大的惯性。 趋势一旦形成，就会持续一段时间，所以基本波动的趋势是可以预测的。

二次波动：周期为3周至3个月的波动，看起来像大海中的波浪，波动幅度约为基本波动幅度的三分之一。 二次波动的方向可以与一次波动的方向相同或相反。 当二级波动方向与基本波动方向相反时，牛市中会形成较大的中期调整，使投资者误认为股市已经开始下跌； 在下跌过程中，会形成大幅反弹，使投资者误认为股市已经开始下跌。 认为股市开始逆转。 因此，二次波动具有很大的欺骗性，很难为股票投资提供准确可靠的科学决策信息。

日波动：几天之内有一个周期的波动，具有很强的随机性和不可预测性，就像海上的涟漪。 虽然日波动幅度不大，但会给基本波动位置和趋势的判断带来很大干扰。 例如，同样是在2005年至2007年的牛市中，上证指数的最大日波动为9%，波动的标准差为3.1%。 但上证指数日均基本波动仅为0.3%。 因此，上证指数的基本面波动完全被每日波动所淹没，人们很难察觉基本面波动的存在。

道氏理论的伟大之处在于，100多年前就发现市场波动是由三个不同的波动周期组成的。 并指出波动的原因来自于投资者的心理行为，并认为基本波动的趋势是可以预测的。 。 由于历史的限制，道氏理论没有提供分析和识别基本波动的方法。

2、股价变动规律

观察股价随时间变化的过程，只有两个变量：股价s和时间t。 对于t的每个值，s都有一个与其对应的唯一值。 因此，股票价格 s 是时间 t 的函数，用 s(t) 表示。

假设 y(t)=ln s(t) 为股票的对数价格（以下简称股价），则 s(t) 在 Delta t 区间内的对数收益率为

\Delta y(t)=y(t)-y(t-\Delta t)(1)

图2显示了上证综合指数及其对数收益率。 从图中可以看出，上证指数下一时刻的对数收益Δy(t)的方向和大小是完全随机且不可预测的，无法用确定性的数学关系来描述。

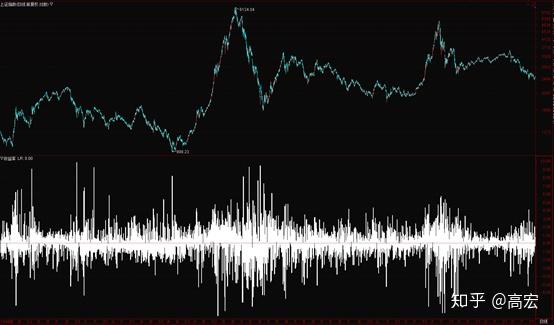
图2 上证综合指数及其对数收益率

2013年诺贝尔经济学奖获得者尤金·法玛在1965年通过对股市的实证检验和分析发现，股市的对数收益是一个零均值不相关的白噪声序列，因此提出了著名的EMH（有效市场假说）有效市场假说。

从式（1）可以看出，股票价格的对数收益是股票对数价格的一阶差分。 因此，基于众多学者对股票对数收益规律的认识，本文提出如下股票价格运动规律：

股票价格运动规律：股票对数价格的一阶差分是零均值不相关的白噪声。

可用的数学公式表示为：

\Delta y(t)=x(t) (2)

其中 x(t) 是零均值不相关白噪声函数。

“白噪声”这个名字来自牛顿。 1666年，牛顿用棱镜证明了太阳发出的白光是振幅相同但频率不同的各种单色光的混合体。 后来，人们把功率谱密度均匀分布在整个频率轴（-∞，+∞）上的函数或信号称为白噪声。

式（2）是用数学语言表达的对股市价格波动规律的理解。 以此为公理，我们可以推导出描述股票价格波动的数学模型以及揭示股票市场周期性波动的幅频特征。

3. 股票价格的数学模型

将式（1）代入式（2），得

y(t)=y(t-\Delta t)+x(t) (3)

假设y(0)=0，反复迭代式(3)即可得到t=N\Delta t时刻的股票价格

y(N)=\sum_{i=1}^{N}{x(i)} (4)

将式(4)视为离散微分方程，可得股价积分模型：

y(t)=\int_{0}^{t}x(t)dt (5)

式（5）的模型参数（积分上限）会随着时间t的变化而变化，因此股票价格的数学模型是一个非线性时变模型。 这就是为什么根据历史股价数据建立的量化模型具有时间敏感性，很快就会失效。 原因之一。

4. 股价的可预测性

根据股价运动规律，股价的差异是不相关的白噪声，因此式（2）中白噪声x(t)的自相关函数为

R_{x}(\tau)=N_{0}\delta (\tau)(6)

式中，τ为时间间隔，N_{0}为正实常数，δ(τ)为单位影响函数。

白噪声x(t)仅在时间间隔τ=0时才相关。 只要两个值之间的时间间隔不为零，它们就彼此不相关，说明股价的变化\Delta y(t)不可预测。

股价的变化\Delta y(t)是不可预测的，但这并不意味着y(t)是不可预测的。 我们可以计算 y(t) 的自相关函数

R_{y}(\tau)=\bar{y(t)y(t-\tau)}

=\int_{0}^{t-\tau}\int_{0}^{t}x(u)x(v)dudy

=\int_{0}^{t-\tau}\int_{0}^{t}x_{0}\delta(uv)dudy

=\int_{0}^{t-\tau}N_{0}du

=N_{0}(t-\tau) (7)

式中，τ为时间间隔。

当τ=0时，R_{y}(τ)具有最大值N_{0}t。 随着 τ 的增加，R_{y}(τ) 线性减小。 当\tau\geq tt时，R_{y}(\tau)=0，说明R_{y}(\tau)在较大范围内有非零值，y(t)随时间变化缓慢，且有很大的惯性，y(t) 存在可以识别和利用的模式，并且它们是可预测的。

在《漫步华尔街》一书中，马尔基尔依靠\Delta y(t)不可预测的结论，直接得出了y(t)也是不可预测的错误判断。 《漫步华尔街》自1973年出版以来，四十多年来一直畅销全球，并已再版11次。 被亚马逊评为畅销书，被誉为近40年来最经典的金融投资入门书籍。 被列为美国MBA学生必读之书。 必读的教学参考书。 《漫步华尔街》中关于股票价格不可预测的错误结论已经误导了人们40多年。

5、股票价格的幅频特性

频域是用来描述事物周期性波动特征的坐标系。 使用傅立叶变换，任何随时间变化的随机运动都可以分解为不同频率的谐波分量，并且每个谐波分量都可以用确定性的正弦或余弦函数表示（图 3）。

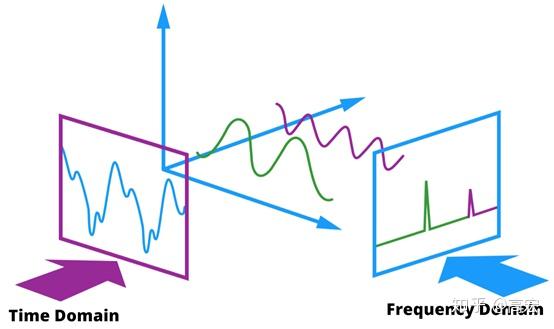
图3 随机波动的频域分解

随机现象虽然不能用时域的确定性数学解析表达式来描述，但可以用频域的确定性数学解析表达式来表达。例如，白噪声的功率谱在频域的解析表达式为

P_{x}(\omega)=N_{0}

式中，N_{0}为正实常数，表示白噪声x(t)的功率谱密度均匀分布在整个频率轴（-∞，+∞）上。 N_{0}的物理意义表示白噪声信号在单位电阻上产生的平均功率。

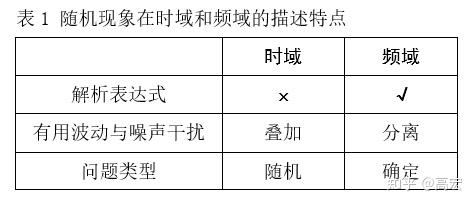
正如文章开头介绍的，股市有四种不同的周期波动：线性趋势、基本波动、次级波动和日波动。 在时域观察股票价格时，这四个不同时期的波动在时间轴上相互叠加。 人们很难察觉线性趋势和基本波动的存在。 他们看到的主要是日波动和次波动。

由于线性趋势、基本波动、二次波动和日波动具有不同的波动频率，因此它们分别位于频率轴的零频、低频、中频和高频频段。 它们在频率轴上相互分离，因此在频域上有很大差异。 很容易发现隐藏在日波动和二次波动中的线性趋势和基本波动，看到从时域角度看不到的波动特征和模式。 因此，频域在信号分析处理技术领域被称为上帝视角。

白噪声x(t)包含所有频率(-∞,+∞)的谐波分量，且各谐波分量的幅值相同。假设谐波分量的幅值为A_{0}，则谐波分量随频率的变化Ω可以表示为A_{0}Cos(Ωt)。 根据式(5)的股价积分模型，可以直接得到 得到频域中ω对应的股价y(t)的幅值

Y(\omega )=\int_{0}^{t}A_{0}Cos(\omega t)dt

=A_{0}\frac{Sin(\omega t)}{\omega}

=A_{0}tSinc(\omega t) (8)

式中，Sinc(\omega t)为Singer函数，是正弦函数Sin(\omega t)与单调递减函数1/\omega t的乘积。

式(8)是股票价格的频域特性，其幅频特性如图4所示。

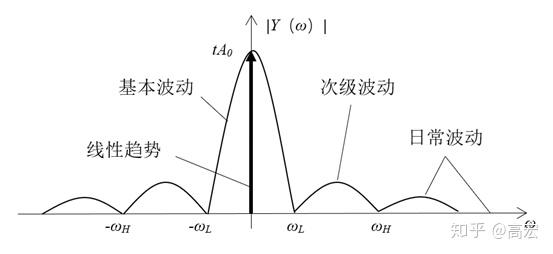
图4 股票价格幅频特征

股价幅频特性Y(ω)表明，经过积分运算后，白噪声就变成了幅频特性与频率成反比的噪声。 其能量主要集中在低频段。 在可见光波段，能量主要集中在最长波长处。 红光，因此这种幅度与频率成反比的噪声称为红噪声。

股票价格的幅频特性Y(Ω)具有以下特点：

(1) Y(Ω) 在 Ω=0 处有最大值，并且与时间 t 成正比。 在时域中，它表示为股票价格y(t)的线性趋势，与时间t成正比。 金属丝。

(2) Sinc函数的主瓣(0